The main objective of my research focusess on different types of equations in the complex domain. These equations are functional equations, differential equations and functional-differential equations. Besides that I am also interested in the algebraic structure of (formal) power series solutions of problems related to associativity and in Decision Theory, and there mainly in the algebraic structure of polynomials.
In the following I want to explain the different areas of my research.
Table of Contents
- Generalized Dhombres Equations in the complex domain
- Briot-Bouquet differential equations and functional-differential equations
- Algebraic aspects of (formal) power series - associative formal power series
- Linear equations and non-linear equations
- Pilgerschritt transform
- Problems in Decision Theory
Generalized Dhombres Equations in the complex domain
The generalized Dhombres equation in the complex domain is given by
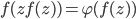
where 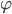 is a given function and
is a given function and 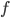 is unknown. One of the origins of this equation refers to a population problem of J. Dhombres, which dates back to 1979 (see [1]). In this setting the equation was first studied in 2005 (see [2]).
is unknown. One of the origins of this equation refers to a population problem of J. Dhombres, which dates back to 1979 (see [1]). In this setting the equation was first studied in 2005 (see [2]).
The task is the determination of all solutions 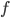 , namely formal, local analytic, entire, meromorphic, algebraic ramified in a point and so on, of the equation for a given
, namely formal, local analytic, entire, meromorphic, algebraic ramified in a point and so on, of the equation for a given 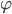 , and to describe the structure of the set of solutions of one of the classes mentioned above.
, and to describe the structure of the set of solutions of one of the classes mentioned above.
Among many other interesting questions one can ask what are normal forms of the Dhombres equation (with respect to an appropriate group of transformations), how can it be treated as a dynamical system in the complex domain, what are all local analytic solutions 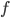 for a given local analytic
for a given local analytic 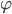 ?
?
For an overview we refer the reader to [3].
[1] J. Dhombres, Some Aspects of Functional Equations, Chulalongkorn University Press, Bangkok, 1979.
[2] L. Reich, J. Smítal, M. Štefánková, Local Analytic Solutions of the Generalized Dhombres Functional Equation I, Sitzungsber. österr. Akad. Wiss. Wien, Math.-nat Kl. Abt. II 214, 3-25 (2005).
[3] L. Reich, J. Tomaschek, Generalized Dhombres equations in the complex domain. A survey, submitted (preprint).
Briot-Bouquet differential equations and functional-differential equations
Briot-Bouquet differential equations in the complex domain are named after C. A. Briot and J.C. Bouquet (see [2]). These are differential equations of the form
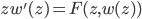
with 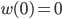 and
and 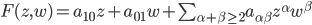 convergent in a sufficiently small neighbourhood of zero. The local analytic solutions
convergent in a sufficiently small neighbourhood of zero. The local analytic solutions 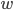 of Briot-Bouquet equations are well-known. For us, the determination of the normal forms of this equation is of great interest. These normal forms are understood with respect to appropriate groups of transformations which transform the class of Briot-Bouquet equations into itself.
of Briot-Bouquet equations are well-known. For us, the determination of the normal forms of this equation is of great interest. These normal forms are understood with respect to appropriate groups of transformations which transform the class of Briot-Bouquet equations into itself.
Nevertheless at the moment we are also interested in functional-differential equations of the form
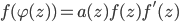
where 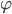 and
and 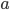 are given and local analytic in a sufficiently small neighbourhood of zero.
are given and local analytic in a sufficiently small neighbourhood of zero.
This type of equations arises from a paper of A. F. Beardon (see [1]) who studied the entire solutions of 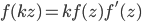 which is a generalization of the equation
which is a generalization of the equation 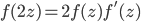 . Obviously
. Obviously 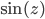 is a solution of the last equation, which justify the research on the generalizations.
is a solution of the last equation, which justify the research on the generalizations.
The functional-differential equation 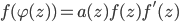 can be transformed to a functional-differential equation of Briot-Bouquet type, that means the transformed equation has similar properties like the Briot-Bouquet differential equation (see [3]).
can be transformed to a functional-differential equation of Briot-Bouquet type, that means the transformed equation has similar properties like the Briot-Bouquet differential equation (see [3]).
Now we are asking wether equations of the type 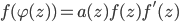 are the only functional-differential equations which can be transformed to an equation of Briot-Bouquet type? Very likely, generalizations of the pantograph equation also lead to functional-differential equations. Furthermore we are interested in normal forms of the original equation.
are the only functional-differential equations which can be transformed to an equation of Briot-Bouquet type? Very likely, generalizations of the pantograph equation also lead to functional-differential equations. Furthermore we are interested in normal forms of the original equation.
[1] A. F. Beardon, Entire Solutions of 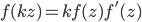 , Comput. Methods. Funct. Theory 12 (2012), 273--278.
, Comput. Methods. Funct. Theory 12 (2012), 273--278.
[2] E. Hille, Ordinary Differential Equations in the Complex Domain, Dover Publications, New York, 1997.
[3] L. Reich, J. Tomaschek, On a functional-differential equation of A. F. Beardon and functional-differential equations of Briot-Bouquet type, Comput. Methods. Funct. Theory, doi: 10.1007/s40315-013-0025-z.
Algebraic aspects of (formal) power series - associative formal power series
One dimensional formal group laws 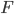 are formal power series
are formal power series 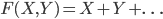 which fulfill the associativity equation
which fulfill the associativity equation
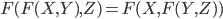 ,
,
(see [2]). In a recent work we determined all associative formal power series 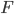 which are not of the form
which are not of the form 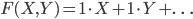 , (see [1]), in the ring of formal power series
, (see [1]), in the ring of formal power series 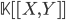 , where
, where 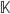 is a commutative field.
is a commutative field.
The question now is the determination of all associative formal power series of dimension 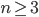 . There are different possibilities to generalize the associativity equation for power series. Namely it can be considered in the sense of formal group laws, or one can discuss it in the meaning of J.-L. Marichal and P. Mathonet (see [3])
. There are different possibilities to generalize the associativity equation for power series. Namely it can be considered in the sense of formal group laws, or one can discuss it in the meaning of J.-L. Marichal and P. Mathonet (see [3])
[1] H. Fripertinger, L. Reich, J. Schwaiger, J. Tomaschek, Associative Formal Power Series in Two Indeterminates, submitted.
[2] M. Hazewinkel, Formal Groups and Applications, Acad. Press, New York and London, 1978.
[3] J.-L. Marichal, P. Mathonet, A description of n-ary semigroups polynomial-derived from integral domains, Semigroup Forum 83 (2011), no. 2, 241-249.
Linear equations and non-linear equations
One of the best known functional equation is the Schröder equation.
For a given 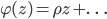 ,
, 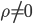 , one has to determine all
, one has to determine all 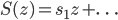 , such that the Schröder equation (or linearization equation)
, such that the Schröder equation (or linearization equation)
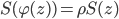
holds.
To obtain solutions  we have to distinguish different values
we have to distinguish different values 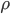 . If
. If 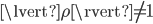 , we obtain an invertible
, we obtain an invertible  such that the linearization equation holds. If
such that the linearization equation holds. If 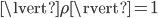 , then there exists an invertible solution
, then there exists an invertible solution  if
if 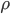 is a Siegel- or Brjuno number (see [2] and [1]).
is a Siegel- or Brjuno number (see [2] and [1]).
Here we ask what can be said about a function  if
if 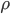 is a root of
is a root of  and
and 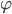 is convergent?
is convergent?
A generalization of this kind of problem is the equation
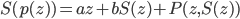
for an unknown  ,
, 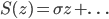 and a known
and a known 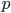 ,
, 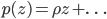 , ord
, ord 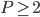 (
(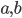 are given complex numbers). The computation of solutions
are given complex numbers). The computation of solutions  which fulfill the generalization is an untouched problem.
which fulfill the generalization is an untouched problem.
Furthermore, if we assume that the order of 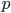 is greater than
is greater than  , what can we say about this generalized equation?
, what can we say about this generalized equation?
[1] A. D. Brjuno, Analytic form of differential equations, Trans. Moscow Math. Soc. 25, 1971, 131-288.
[2] C. L. Siegel, Vorlesungen über Himmelsmechanik, Springer, Berlin, 1956.
Pilgerschritt transform
The idea of the Pilgerschritt transform is the following, we demonstrate it for the complex affine group 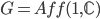 , see [2]:
, see [2]:
Let 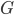 be the above mentioned group with unit element
be the above mentioned group with unit element 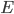 . Let
. Let 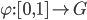 be a
be a 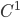 -path where
-path where 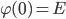 .
.
Then we define 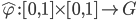 as the solution of the differential equation
as the solution of the differential equation
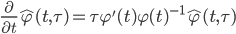 with
with 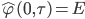 .
.
Then we get a new path 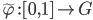 by putting
by putting  .
. 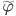 fulfills the following:
fulfills the following:
1.) 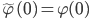 ,
, 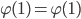 ,
,
2.) 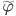 is an analytic function,
is an analytic function,
3.) if 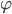 is the restriction of a one-parameter-subgroup to the intervall
is the restriction of a one-parameter-subgroup to the intervall 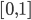 , then
, then 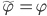 .
.
Then we define the sequence 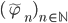 inductively by
inductively by
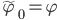 ,
, 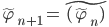 .
.
This sequence is called the sequence of the Pilgerschritt transform of 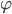 (or Pilgerschritt sequence of
(or Pilgerschritt sequence of 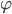 ).
).
Therefore the problem is the investigation of the convergence of this sequence.
[1] W. Förg-Rob, The Pilgerschritt transform in Lie algebras, Iteration theory and its functional equations, Proc. Int. Symp., Schloß Hofen (Lochau)/Austria 1984, Lect. Notes Math. 1163, 59-71 (1985).
[2] W. Förg-Rob, Some results on the Pilgerschritt transform, European conference on iteration theory. Proceedings of the conference, ECIT '87, 198-204 (1987).
[3] W. Förg-Rob, N. Netzer, Product-integration and one-parameter subgroups of linear Lie-groups, Iteration theory and its functional equations, Proc. Int. Symp., Schloß Hofen (Lochau)/Austria 1984, Lect. Notes Math. 1163, 72-82 (1985).
[4] Ch. Winklmair, Konvergenzverhalten des Pilgerschrittverfahrens in der Affinen Gruppe 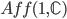 , Diploma Thesis, Leopold-Franzens-Universität Innsbruck, 2010.
, Diploma Thesis, Leopold-Franzens-Universität Innsbruck, 2010.
Problems in Decision Theory
Recently my attention was drawn to problems occuring in Decision Theory. Here we mainly investigate algebraic properties of polynomials. For an introduction to this topic we refer the reader to the book [1] of my present PostDoc supervisor J.-L. Marichal and his colleagues.
[1] M. Grabisch, J.-L. Marichal, R. Mesiar, E. Pap, Aggregation Functions, Cambridge University Press, Cambridge, 2009.
